What is Digital signature algorithm (DSA)?

Updated on : 2020-Nov-19 15:45:51 | Author :

Contents

 

  • Cryptographic techniques for creating a Digital Signature Algorithm
  • What is the Digital Signature Algorithm or DSA

 

Cryptography is a mathematical method used for encryption-decryption purposes.

Cryptographic techniques

Cryptographic techniques can be divided into three subtypes. They are-

 

  • Symmetric-key cryptography

The sender and the receiver both of them share a single key. The sender generally encrypts plain text data with this key and then sends the cipher data to the receiver. Thereafter the receiver decrypts the message with the same key and recovers the plain text format.

 

  • Hash functions

​​​​​​​In the hash function, no key is used. A hash value of a fixed length is computed according to the plain text. This hash function is used to encrypt passwords by many operating systems.

 

  • Public-key cryptography

​​​​​​​In the public-key cryptography method, two related keys called a private key and personal key are used. The public key is paired with the private key that is a secret key. The public key cryptography is used to encrypt and the private key is used to decrypt.

 

What is the Digital Signature Algorithm or DSA

  • Firstly, each person who adopts this scheme has a public-private key pair to encrypt and decrypt in cryptography.

  • The key pairs used for encryption or decryption and signing or verifying are different for every signature. Here, the private key used for signing is referred to as the signature key and the public key as the verification key in this algorithm.

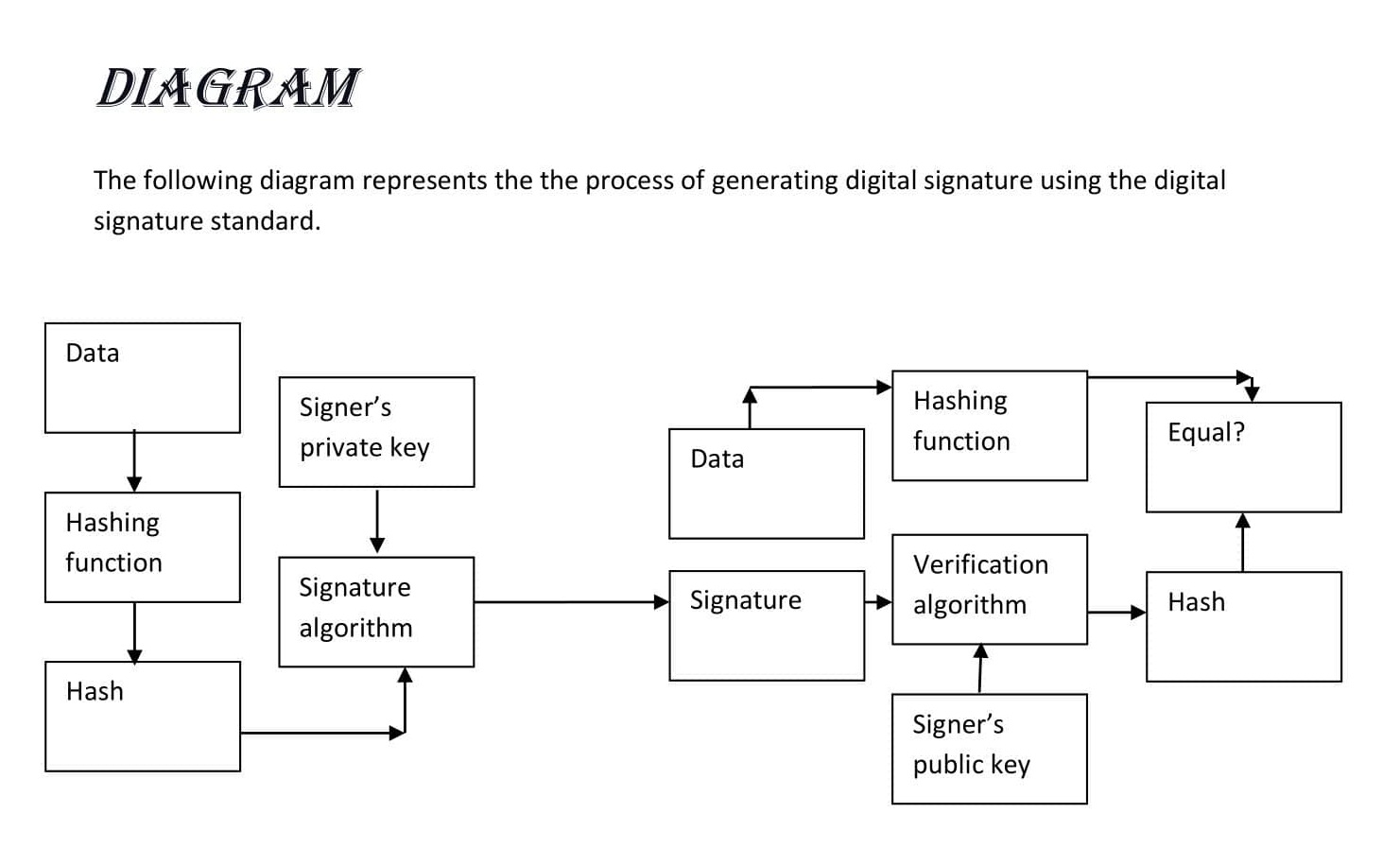
  • Then, people take the signer feeds data to the hash function and generates a hash of data of that message.

  • Now, the Hash value and signature key are then fed to the signature algorithm which produces the digital signature on a given hash of that message. This signature is appended to the data and then both are sent to the verifier to secure that message.

  • Thereafter the verifier puts the digital signature and the verification key into the algorithm of this Digital Signature Algorithm. Thus, the verification algorithm provides some value as the output is called ciphertext.

  • Thus, the verifier also runs the same hash function on received data to generate hash value in this algorithm.

  • Now, for verification, the signature, this hash value, and the output of the verification algorithm are compared with each variable. Based on the comparison result, the verifier decides whether the digital signature is valid for this or invalid.

  • Therefore, the digital signature is generated by the 'private' key of the signer and no one else can have this key to secure the data, the signer cannot repudiate signing the data in the future for securing that data by the cryptographic method

 

A digital signature algorithm or DSA steps

 

 

The main thing of the digital signature algorithm is the public key and private key generation through the following steps, which can be told as:

 

  • Firstly, choose a prime number q, which is called the prime divisor in this.

  • Then, choose another primer number p, such that p-1 mod q = 0. p is called the prime modulus in this.

  • Then, choose an integer g, such that 1 < g < p, g**q mod p = 1 and g = h**((p–1)/q) mod p. q is also called g's multiplicative order modulo p in this algorithm.

  • Then, choose an integer, such that 0 < x < q for this.

  • Now, compute y as g**x mod p.

  • Thus, Package the public key as {p, q, g, y} is this.

  • Package the private key as {p, q, g, x} is this regard.

Then, the second thing of the digital signature algorithm is the signature generation process and signature verification process in this algorithm, which can be told as:

Firstly, for generating a message signature, the sender can follow these steps:

 

  • Firstly, initiate the message digest called h by using a hash algorithm like SHA1.

  • Then, generate a random number k, such that 0 < k < q.

  • Then, Computer as (g**k mod p) mod q. If r = 0, select a different k.

  • Thereafter Compute I, such that k*i mod q = 1. i is called the modular multiplicative inverse of k modulo q in this method.

  • Thereafter Compute s = i *(h + r*x) mod q. If the value of s = 0, then select a different k.

  • Thus, the Package of the digital signature as {r and s}.

Then, to verify a message signature, the receiver of the message and the digital signature can follow these further steps as:
​​​​​​​

  • Firstly, initiate the message digest h, using the same hash algorithm.

  • Then, Compute w, such that s*w mod q = 1. w is called the modular multiplicative inverse of s modulo q in this.

  • Then, Compute u1 = h*w mod q.

  • And, Compute u2 = r*w mod q.

  • Then, Compute v = (((g**u1)*(y**u2)) mod p) mod q.

  • Wherever, If v == r, the digital signature is valid.

 

 

 

 

Additional resources

 

Get FREE Advice